목차
1. 사이킷런 Linear Regression을 이용한 보스턴 주택 가격 예측
1. 사이킷런 Linear Regression을 이용한 보스턴 주택 가격 예측
class sklearn.linear_model.LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=1)- 입력 파라미터
- fit_intercept : 불린 값으로, 디폴트는 True, Intercept(절편) 값 계산할지 말지 지정.
False로 지정하면 intercept가 사용되지 않고 0으로 지정됨.
- normalize : 불린 값으로, 디폴트는 False. fit_intercept가 False인 경우에는 이 파라미터가 무시됨.
True이면 회귀를 수행하기 전에 입력 데이터 세트를 정규화
- 속성
- coef_
fit() 메서드로, X,y 배열을 입력받으면 회귀 계수인 W를 coef_속성에 저장함.
회귀 계수가 배열 형태로 저장하는 속성. shape는 (Target 값 개수, 피처개수)
- intercept_
이 회귀 계수 계산은 입력 피처의 독립성에 많은 영향을 받음.
피처 간의 상관 관계가 매우 높은 경우, 분산이 매우 커져서 오류에 매우 민감해짐.(많이 떨어져 있으니까, 개별 추정값들이 크게크게 바뀜) ⇒ “다중 공선성” 문제
→ 상관 관계가 높은 피처가 많은 경우 독립적인 중요한 피처만 남기고 제거하고나 규제를 적용함.
→ 매우 많은 피처가 다중 공선성 문제를 가지고 있다면 PCA를 통해 차원 축소 고려
2. 편향과 분산
1) 편향이란? → 중심과 떨어져 있는지 아닌지
편향이란, (노이즈가 다른) 여러 데이터셋을 바탕으로 추정값들의 중심(노란색의 중심)이 얼마나 실제 데이터의 중심(정답)과 떨어져 있는가를 의미하는 것이다. 편향이 작다는 뜻은 여러 데이터셋을 바탕으로 반복적으로 추정하는 과정을 통해 전체적인 오차를 줄일 수 있다는 뜻이다. 반면에, 편향이 크다는 것은 아무리 노력을 해도 정답을 맞출 가능성이 적다는 뜻이다.
2) 분산이란? → 데이터들끼리 모여있는지 아닌지 (분산 높으면 떨어져 있다는 거)
분산이란, (노이즈가 다른) 여러 데이터셋을 바탕으로 추정한 결과들이 그 결과들의 평균과 비교했을 때 얼마나 퍼져 있는가를 나타낸다. 분산이 작으면 노이즈가 변한다고 해서 함수의 추정값이 크게 바뀌지 않는다는 뜻이다. (f_hat(x)들끼리 모여있으니까!) 반면에 분산이 크면, 노이즈가 바뀔수록 개별적인 추정값들이 크게크게 바뀐다는 뜻이다.
3) 모델의 4가지 유형
편향과 분산 정도에 따라 학습 모델을 [그림 3]과 같이 4가지 유형으로 분류해 볼 수 있다.

1️⃣ 높은 편향, 높은 분산: 정확도가 떨어지는 가장 쓸모 없는 유형이다.
2️⃣ 낮은 편향, 높은 분산: 추정값들이 전체적으로 정답에 가깝지만 자기들끼리는 분산되어 있는 유형이다. (Decision Tree, ANN, SVM, k-NN with small k 등)
3️⃣ 높은 편향, 낮은 분산: 추정값들끼리는 모여있지만, 전체적으로 정답과 거리가 있는 유형이다. (Logistic Regression, LDA, k-NN with large k 등)
4️⃣ 낮은 편향, 낮은 분산: 추정값들끼리 모여있으면서 동시에 정답에 가까운 유형으로 가장 바람직하다.
3. 회귀 평가 지표
실제값과 예측값의 차이를 그냥 더하면 +와 -가 섞여서 오류 상쇄되므로 절댓값 평균이나 제곱, 제곱한 뒤 루트 씌운 평균값으로 구함.
1) RSS - 단순 오차
실제 값과 예측 값의 단순 오차 제곱 합. 값이 작을수록 모델의 성능이 높음. 전체 데이터에 대한 실제 값과 예측하는 값의 오차 제곱의 총합.

2) MAE(Mean Absolute Error)
평균 절댓값 오차. 실제 값과 예측값의 차이를 절댓값으로 편환해 평균 한 것.

변동성이 큰 지표와 낮은 지표를 같이 예측할 시 유용.
3) MSE(Mean Squeared Error)
평균 제곱 오차. 실제 값과 예측값의 차이를 제곱해 평균한 것,(RSS에서 데이터 수만큼 나눈 값)

이상치 즉, 데이터들 중 크게 떨어진 값에 민감함.
4) RMSE
MSE값은 오류의 제곱을 구하므로 실제 오류 평균보다 더 커지는 특성이 있으므로 MSE에 루트 씌운 것
5) R제곱(결정계수)
분산 기반으로 예측 성능을 평가함. 실제 값의 분산 대비 예측값의 분산 비율을 지표로 하며, 1에 가까울수록 예측 정확도가 높음.
예측값 variance / 실제값 variance
R2= 1 - RSS/TSS
**TSS는 데이터 평균 값과 실제 값 차이의 제곱

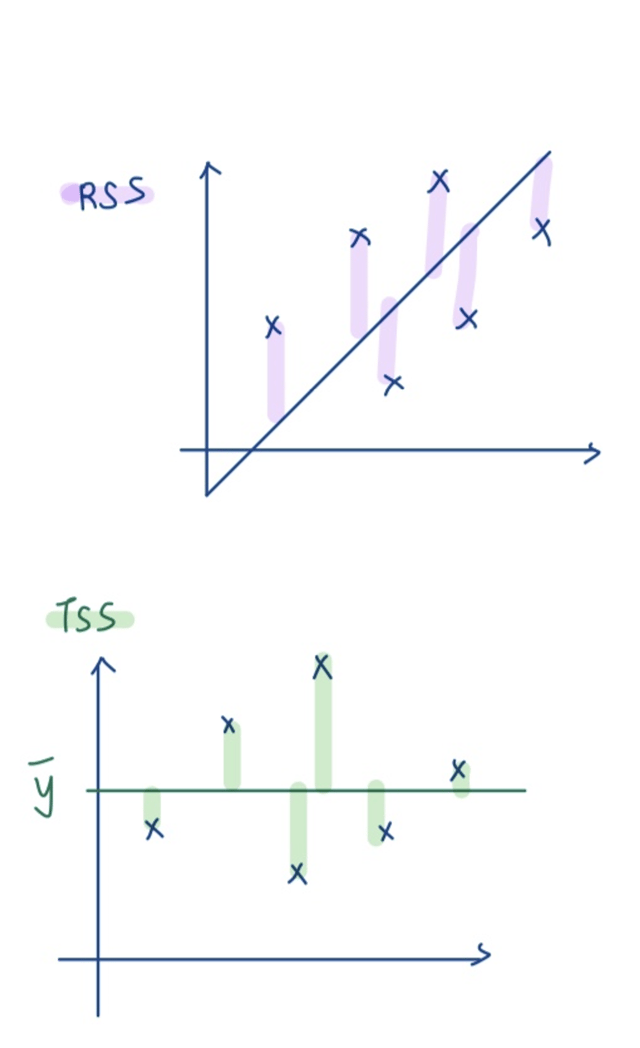
R2 값이 0인 경우, 데이터의 평균 값을 출력하는 직선 모델을 의미함. (RSS/TSS가 1인거고, 그건 RSS와 TSS가 같다는 거니까.)
** 위 지표들은 사이킷런에서 적용할 때 ‘neg_’, ‘-1’을 붙임
→ 사이킷런의 scoring 함수가 score값이 클수록 좋은 평가 결과로 자동 평가하기 때문.
but, 실제 값과 예측 값의 오류 차이를 기반으로 하는 회귀 평가 지표의 경우 값이 커지면 오히려 나쁜 모델이라는 의미이므로, -1을 원래의 평가 지표 값에 곱해서 음수를 만들어 작은 오류 값이 더 큰 숫자로 인식하게 함.
'Machine Learning > 회귀' 카테고리의 다른 글
| [파이썬 머신러닝 가이드] 회귀 - 다항 회귀와 과(대)적합/과소적합 이해 (1) | 2023.12.23 |
|---|---|
| [파이썬 머신러닝 가이드] 회귀 - 경사 하강법(Gradient Descent) (1) | 2023.12.23 |
| [파이썬 머신러닝 가이드] 회귀 - 회귀 소개 (1) | 2023.12.23 |

