이번 BITAmin 시계열 프로젝트에서 강화학습을 이용한 주식 실시간 트레이딩을 진행하게 되었는데, 프로젝트를 본격적으로 시작하기 전에 공부했던 강화학습의 개념에 대해 정리하고 가고자 한다.
강화학습은 마르코프 의사결정 과정에 학습에 개념을 넣은 것인데, 이번 포스팅에서는 강화학습 뿐만 아니라 많은 모델들의 기본이 되기도 하는 마르코프 의사 결정 과정에 대해 정리해보고자 한다.
먼저,
강화학습이란,
머신러닝의 한 종류로, 어떠한 환경에서 어떠한 행동을 했을 때 그것이 잘 된 행동인지 잘못된 행동인지를 나중에 판단하고 보상 (또는 벌칙)을 줌으로써 반복을 통해 스스로 학습하게 하는 분야이다.
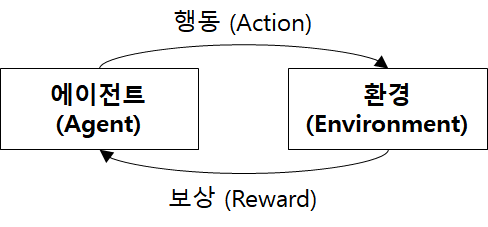
그림을 보면 알 수 있듯이 강화학습의 두 가지 구성요소는 환경과 에이전트이다.
- 에이전트 : 특정환경에서 행동을 결정
- 환경 : 그 결정에 대한 보상을 내림
(이 보상은 행동이 즉시 결정되기 보다는 여러 행동을 취한 후에 한꺼번에 결정되는 경우가 많다.)
-> 에이전트가 행동을 결정하고 환경이 주는 보상으로 스스로 학습할 때 주로 딥러닝에서 다룬 인공 신경망을 사용한다.
환경과 에이전트 상태 등을 입력값으로 받아 인공 신경망이 행동을 결정하고,
보상이 있으면 이전의 입력값과 행동들을 긍정적으로 학습한다.
강화학습의 기초가 된 마르코프 의사 결정 과정
1) 마르코프 가정
마르코프 가정은 상태가 연속적인 시간에 따라 이어질 때 어떠한 시점의 상태는 그 시점 바로 이전의 상태에만 영향을 받는다는 가정이다.
( 현재 상태는 이전 상태에 가장 큰 영향을 받고, 이전 상태는 그 이전 상태에 가장 큰 영향을 받고....의 반복 !!)
P(St | S1, S2, … , St-1) = P(St | St-1)
- 좌변 : 어떠한 시점 t에서의 상태 St는 최초의 상태 S1에서 바로 이전의 상태 St-1까지의 영향을 받는다는 뜻
-> 연속적으로 존재하며 일어나는 일련의 상태들을 확실하게 표현하지만, 실제로 계산하기 어렵다.
- 우변 : 상태 St는 바로 이전 상태인 St-1에 가장 큰 영향을 받고, St-1에서 St-2를 반영하는 등 연쇄적으로 모든 이전 상태가 반영된다고 가정하는 마르코프 가정을 적용한 단순한 version!
2) 마르코프 과정
마르코프 과정 (Markov decision process, MDP)은 마르코프 가정을 만족하는 연속적인 일련의 상태이다.
마르코프 과정은 일련의 상태 <S1, S2, … , St> 와 상태 전이 확률 P로 구성된다.
- 상태 전이 확률

여기서 P(A|B) 는 조건부 확률로 B일 때 A일 확률을 의미한다.
(마르코프 가정을 반영했기 때문에 이렇게 계산 가능한 상태 전이 확률 정의가 가능한 것임
-> P(St | St-1) 생각하면, 조건부 확률로 St-1일 때 St일 확률 )
3) 마르코프 의사 결정 과정
마르코프 의사 결정 과정은 마르코프 과정을 기반으로 한 의사 결정 모델을 말한다.
MDP는 상태(state) 집합 S, 행동(action) 집합 A, 상태 전이 확률 행렬 P, 보상 함수 R, 할인 요인 r로 구성되어 있다.
MDP = (S, A, P, R, r)
- 상태 집합은 MDP에서 가질 수 있는 모든 상태 집합 S={s1,s2,…,s|S|} (St = s, s∈S)
-> 어떠한 시점에서의 상태 St는 상태 집합 S에 포함된 특정 상태가 됨
- 행동 집합은 행동 주체인 에이전트가 할 수 있는 모든 행동의 집합 A = {a1, a2, ..., a|A|}이다.
(At = a, a∈A)
- 상태전이 확률 (MDP에서의, 그냥 마르코프 과정의 상태전이확률에 a, 행동 집합 추가)
P(s’ | s,a) = P[St+1 = s’ | St = s, At = a]
P(s’ | s,a) 는 에이전트가 어떠한 상태 s에서 행동 a를 취했을 때 상태 s’으로 변할 확률
- 보상함수는 에이전트가 어떠한 상태에서 취한 행동에 대한 보상을 내리기 위한 함수
R(s,a) = E[Rt+1 | St = s, At = a]
상태 s에서 행동 a를 했을 때의 보상의 기댓값을 수치로 반환한다.
- 할인 요인은 과거의 행동을 얼마나 반영할지를 정하는 값으로 0에서 1사이의 값
ex) 과거 5번의 행동에 대한 보상을 1씩 받았다고 할 때,
- 할인 요인 r이 1이면
<1,1,1,1,1>
- 할인 요인 r이 0.9이면
<1, 0.9, 0.81, 0.729, 0.6561> ← 앞에거 두개 곱한게 다음 값이다.
- 정책
에이전트는 어떠한 상태 s에서 수행할 행동 a를 정해야하는데, 이를 정책이라 한다.
π(a|s) = P[At = a | St = s]
정책은 총 보상을 최대화하는 방향으로 갱신된다!!!

ex) P(s2 | s1,a2) =1로, s1에서 a2를 수행하면 s2가 된다.
에이전트는 정책에 따라 행동을 결정하고 함정에 다다르면 -0.1을 보상으로 주고, 목적지에 다다르면 1을 보상으로 주어 정책을 조정해 나간다.
출발점 s1에서 a2를 두 번 취해 s3가 되면 -0.1을 보상으로 주는데, 이때 π(a2 | s1)과 π(a2 | s2)의 값을 다시 똑같이 함정에 빠지지 않는 방향으로 갱신한다.
- π(a2 | s1) = π(a2 | s1) x (1 - 0.1 x 0.9)
- π(a2 | s2) = π(a2 | s2) x (1 - 0.1 x 1)
s2에서 s3로 이동한 게 가장 최근 행동이므로 보상을 그대로 주고, 그 전의 행동인 s1에서 s2로 이동한 건 할인 요인 0.9를 곱해 보상 반영한다.
⇒ 함정이 아니라 목적지에 다다르면 취했던 행동들의 확률값이 높아진다.
⇒ 정책이 함정을 피하며 목적지로 갈 수 있게 조정된다.

