[파이썬 머신러닝 가이드] 차원 축소 - SVD

목차

1. 차원 축소 개요

2. SVD

 

1. 차원 축소(Dimension Reduction) 개요

• 일반적으로 차원이 증가할수록 데이터 포인트 간의 거리가 기하급수적으로 멀어지게 되고, 희소한 구조를 가지게 됨.
• 수백 개 이상의 피처로 구성된 데이터 세트의 경우 상대적으로 적은 차원에서 학습된 모델보다 예측 신뢰도가 떨어짐.
• 피처가 많을 경우 개별 피처 간에 상관관계가 높을 가능성이 크고, 선형모델에서 입력 변수 간의 상관관계가 높을 경우 다중공선성 문제로 예측 성능이 저하됨.

1. 피처 선택

: 특성 선택, 특정 피처에 종속성이 강한 불필요한 피처는 아예 제거, 데이터의 특징을 잘 나타내는 주요 피처만 선택.

1. 피처 추출

특성 추출, 기존 피처를 저차원의 중요 피처로 압축해서 추출하는 것. 새롭게 추출된 중요 특성은 기존의 피처가 압축된 것이므로 기존의 피처와는 완전히 다른 값.

** 피처를 함축적으로 더 잘 설명할 수 있는 또 다른 공간으로 매핑해 추출하는 것.

함축적 피처 추출 : 기존 피처가 전혀 인지하기 어려웠던 잠재적 요소를 추출하는 거.

→ 이미지 분류 등 분류에서 과적합 영향력 작아짐 ( 이미지 자체가 가지고 있는 차원의 수가 너무 크면 비슷한 이미지라도 적은 픽셀 차이가 잘못된 예측으로 이어질 수 있음)

→ 텍스트 문서의 숨겨진 의미를 추출할 때. ( 많은 단어로 구성되어 있는 문서에서, 숨겨져 있는 시맨틱의 의미나 토픽을 잠재 요소로 간주하고 이를 찾아낼 수 있음 - SVD, NMF)

 

2. SVD(Singular Value Decomposition)

- 여기서 U와 V는 orthogonal matrix (직교행렬)이어야하고, Σ는 diagonal matrix(대각행렬)이어야함.

 

** 두 벡터가 orthogonal 하거나 orthonormal 하다는 것은?

1. orthogonal : 두 벡터가 직교. 내적이 0일 때 ⇒ U·V = 0
2. orthonormal : 두 벡터가 orthogonal + 둘다 unit(크기가 1인 벡터일 때) ⇒ U·V = 0 , ||u|| = ||v|| = 1

 

** 한 행렬이 orthogonal 하다는 것은?

모든 column vector들이 서로 orthonormal할 때.

 

** diagonal matrix (대각 행렬이란?)

: N x N square matrix에서, 대각선에만 값이 존재하고, 나머지 위치의 값은 0인 것.

 

• SVD

r은 rank개 만큼.

U에 대해서… UTU = I

=> 따라서 UT는 U-1(U의 역행렬임)

UT - 자기 자신 말고 다른 애들이랑 다 곱했을 때 그 inner product는 다 0이 되고, 자기자신이랑 곱했을 때만 1이라는 값을 가짐. → 자기 자신의 크기가 1이고, 나머지 열벡터들과는 orthogonal 함.

 

I - 주대각선 성분은 다 1, 나머지는 다 0

 

 

 

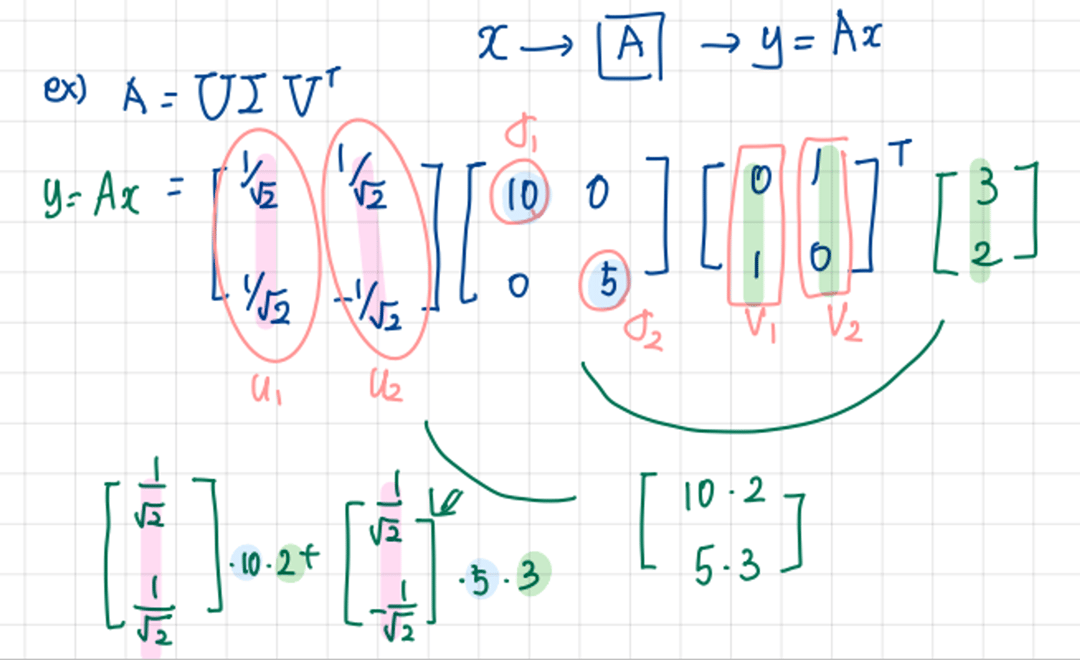
** x를 V의 column에다 inner product를 취해주고, 대각행렬인 Σ안에 있는 원소들로 스케일링을 해준후, U와 linear combination을 해주며 span 해준다.

 

U에 방향이 담겨있고, Σ안에 원소들 σ1, σ2에 그 크기가 담겨있다.

 

v라는 성분을 얼마나 가지고 있는지 체크하고, σ만큼 늘리고 줄이는 과정을 거쳐서 v라고 하는 새로운 공간을 표현하는 기저벡터에 얹어서 표현.

 

 

 

 

 

• A 행렬 대각화 사용하여 SVD 분해하는 법

대각화를 사용하면, A = PDP-1(P-1은 P의 역행렬) 로 대각화처럼 분해할 수 있는데, 이 속성을 이용하여 AAT를 U(ΣΣT)U-1로, ATA를 V(ΣΣT)V-1로 분해.

A= UΣVT이니까, AT는 VΣTUT이고, 각각 AAT, ATA 계산하면 위에처음 분해 가능함. U와 V는 orthogonal 하기 때문에 UTU와 VTV는 I(identity matrix)이니까 없애면,

UT = U-1, VT=V-1이기 때문에 U(ΣΣT)UT, V(ΣΣT)VT를 U(ΣΣT)U-1, V(ΣΣT)V-1이렇게 표현 가능한 것.

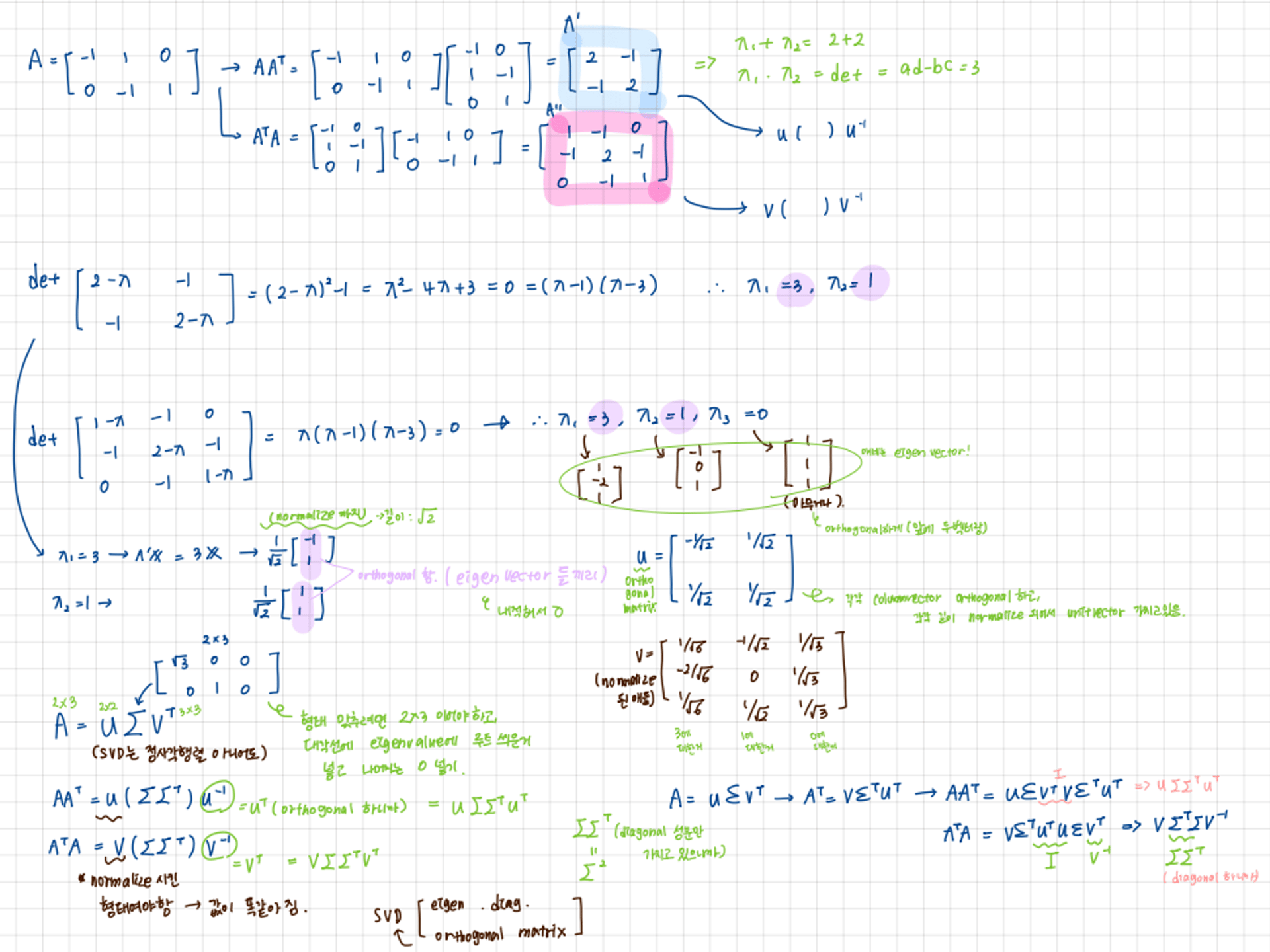
SVD는 정방행렬 뿐만 아니라 행과 열의 크기가 다른 행렬(직사각행렬)에도 적용할 수 있음.

 

A = UΣVT에서,

행렬 U와 V에 속한 벡터는 특이벡터(singular vector, AAT와 ATA의 eigenvector)이며, 모든 특이벡터는 서로 직교(orthogonal)하는 성질을 지님.

Σ는 대각행렬이며, Σ이 위치한 0이 아닌 값이 바로 행렬 A의 특이값(singular value, eigenvalue에 루트씌운거)임.

A의 차원이 m x n 일 때, U의 차원이 m x m, Σ의 차원이 m x n, VT의 차원이 n x n으로 분해됨.

 

일반적으로는, Σ의 비대각인 부분과 대각원소 중에 특이값이 0인 부분도(더 큰 행렬에선 겹치는 eigen value 아니면 0처럼 쓸데없는 값임) 모두 제거하고 제거된 Σ에 대응되는 U와 V원소도 함께 제거해 차원을 줄인 형태로 SVD를 적용함.

→ 컴팩트한 형태로 SVD 적용하면(Truncated SVD), A의 차원이 m x n일 때 U의 차원을 m x p, Σ의 차원을 p x p, VT의 차원을 p x n으로 분해함.

 

• Truncated SVD

: Σ의 대각 원소 중에 상위 몇 개만 추출해서 여기에 대응하는 U와 V의 원소도 함께 제거해 더욱 차원을 줄인 형태로 분해하는 것.

 

• SVD 분해는 numpy.linalg.svd에 파라미터로 원본행렬을 입력하면 U, sigma, V 전치 행렬을 반환함.

sigma 행렬은 Σ행렬의 0이 아닌 경우만 1차원 행렬로 표현함.

 

# numpy의 svd 모듈 import
import numpy as np
from numpy.linalg import svd

# 4X4 Random 행렬 a 생성 
np.random.seed(121)
a = np.random.randn(4,4)
print(np.round(a, 3))

U, Sigma, Vt = svd(a)
print(U.shape, Sigma.shape, Vt.shape)
print('U matrix:\n',np.round(U, 3))
print('Sigma Value:\n',np.round(Sigma, 3))
print('V transpose matrix:\n',np.round(Vt, 3))

(4, 4) (4,) (4, 4)
U matrix:
 [[-0.079 -0.318  0.867  0.376]
 [ 0.383  0.787  0.12   0.469]
 [ 0.656  0.022  0.357 -0.664]
 [ 0.645 -0.529 -0.328  0.444]]
Sigma Value:
 [3.423 2.023 0.463 0.079]
V transpose matrix:
 [[ 0.041  0.224  0.786 -0.574]
 [-0.2    0.562  0.37   0.712]
 [-0.778  0.395 -0.333 -0.357]
 [-0.593 -0.692  0.366  0.189]]

분해된 U, sigma, Vt를 이용해 원본행렬로 복원하려면 내적하면 됨,(sigma는 0이 아닌 값만 1차원으로 추출했으므로 다시 0을 포함함 대칭행렬로 변환한 뒤에 내적을 수행해야 함)

 

# Sima를 다시 0 을 포함한 대칭행렬로 변환
Sigma_mat = np.diag(Sigma)
a_ = np.dot(np.dot(U, Sigma_mat), Vt)
print(np.round(a_, 3)) # -> 동일하게 복원됨

 

**np.diag 기능

1. 대각행렬 생성 기능 : v가 1차원 배열일때, v를 대각행렬로 하는 2차원 배열을 만들어줌
2. 대각요소 추출 기능 : v가 2차원 배열일때, v의 대각선 요소들을 1차원으로 뽑아줌

+만약, 로우 간의 의존성이 높다면, SVD로 분해했을 때 sigma 값 중 2개가 0으로 변함.

즉, 선형 독립인 로우 벡터의 개수가 2개라는 의미.(행렬의 rank가 2)

→ 이 경우엔 복원할 때 U 행렬의 경우는 sigma와 내적을 수행하므로 sigma의 앞 2행에 대응되는 앞 2열만 추출,

V 전치행렬의 경우는 앞 2행만 추출해 복원.

 

• Truncated SVD를 이용해 행렬 분해

특이값 중 상위 일부 데이터만 추출해 분해하기 때문에 인위적으로 더 작은 차원으로 분해되어 원본 행렬을 정확하게 다시 원복할 수는 없음.

그래도 상당 수준 근사 가능.

→ 사이파이 이용. 사이파이의 truncated svd는 희소 행렬로만 지원돼서 scipy.sparse.linalg.svds를 이용해야함

num_components에 추출하길 원하는 sigma 행렬의 특이값 개수로 지정하고 변환 수행 → (6,4), (4,), (4,6)

 

+사이킷런의 truncatedSVD 클래스는 U,sigma, Vt 행렬을 반환하진 않고, PCA 클래스와 유사하게 fit과 transform 호출해 원본 데이터를 몇 개의 주요 컴포넌트 (Truncated SVD의 K 컴포넌트 수)로 차원을 축소해 변환함.

원본 데이터를 Truncated SVD 방식으로 분해된 U*sigma 행렬에 선형 변환하여 생성

from sklearn.decomposition import TruncatedSVD, PCA
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline

iris = load_iris()
iris_ftrs = iris.data
# 2개의 주요 component로 TruncatedSVD 변환
tsvd = TruncatedSVD(n_components=2)
tsvd.fit(iris_ftrs)
iris_tsvd = tsvd.transform(iris_ftrs)

# Scatter plot 2차원으로 TruncatedSVD 변환 된 데이터 표현. 품종은 색깔로 구분
plt.scatter(x=iris_tsvd[:,0], y= iris_tsvd[:,1], c= iris.target)
plt.xlabel('TruncatedSVD Component 1')
plt.ylabel('TruncatedSVD Component 2')

from sklearn.preprocessing import StandardScaler

# 붓꽃 데이터를 StandardScaler로 변환
scaler = StandardScaler()
iris_scaled = scaler.fit_transform(iris_ftrs)

# 스케일링된 데이터를 기반으로 TruncatedSVD 변환 수행 
tsvd = TruncatedSVD(n_components=2)
tsvd.fit(iris_scaled)
iris_tsvd = tsvd.transform(iris_scaled)

# 스케일링된 데이터를 기반으로 PCA 변환 수행 
pca = PCA(n_components=2)
pca.fit(iris_scaled)
iris_pca = pca.transform(iris_scaled)

# TruncatedSVD 변환 데이터를 왼쪽에, PCA변환 데이터를 오른쪽에 표현 
fig, (ax1, ax2) = plt.subplots(figsize=(9,4), ncols=2)
ax1.scatter(x=iris_tsvd[:,0], y= iris_tsvd[:,1], c= iris.target)
ax2.scatter(x=iris_pca[:,0], y= iris_pca[:,1], c= iris.target)
ax1.set_title('Truncated SVD Transformed')
ax2.set_title('PCA Transformed')

 

+데이터 세트가 스케일링으로 데이터 중심이 동일해지면 사이킷런의 SVD와 PCA는 동일한 변환 수행.

→ PCA가 SVD 알고리즘으로 구현됐음을 의미. (PCA는 밀집행렬에 대한 변환만 가능, SVD는 희소행렬에 대한 변환도 가능)