[파이썬 머신러닝 가이드] 차원축소 - LDA, NMF

목차

1. LDA

2. NMF

 

1. LDA(Linear Discriminant Analysis)

LDA는 선형 판별 분석법으로 불리며, PCA와 유사

둘 다 입력 데이터 셋을 저차원 공간에 투영해 차원을 축소하는 기법이지만,

중요한 차이는 LDA는 지도학습의 분류에서 사용하기 쉽도록 개별 클래스를 분별할 수 있는 기준을 최대한 유지하면서 차원을 축소함.

PCA는 입력 데이터의 변동성이 가장 큰(분산이 큰) 축을 찾았지만, LDA는 입력 데이터의 결정값 클래스를 최대한으로 분리할 수 있는 축을 찾음

→ LDA 구할 때 가장 큰 타이점은 공분산 행렬이 아니라, 클래스 간 분산과 클래스 내부 분산 행렬을 생성한 뒤, 이 행렬에 기반해 고유벡터를 구하고 입력 데이터를 투영함.

** LDA는 실제로는 PCA와 다르게 비지도학습이 아닌 지도학습임!

→ 클래스 결정값이 변환 시에 필요.(lda 객체의 fit()메서드 호출할 때 결정값이 입력됨 (ex. lda.fit(iris_scaled, iris.target))

 

LDA

→ 특정 공간상에서 클래스 분리를 최대화하는 축을 찾기 위해 클래스 간 분산과 클래스 내부 분산의 비율을 최대화 하는 방식으로 차원 축소

(클래스 간 분산은 최대한 크게, 클래스 내 분산의 최대한 작게)

 

• LDA 구하는 스텝

1. 클래스 내부와 클래스 간 분산 행렬 구함. 이 두 개 행렬은 입력 데이터의 결정 값 클래스별로 개별 피처의 평균 벡터를 기반으로 구함.

2. 클래스 내부 분산 행렬을 Sw, 클래스 간 분산 행렬을 Sb라고 하면 다음 식으로 두 행렬을 고유벡터로 분해할 수 있음.

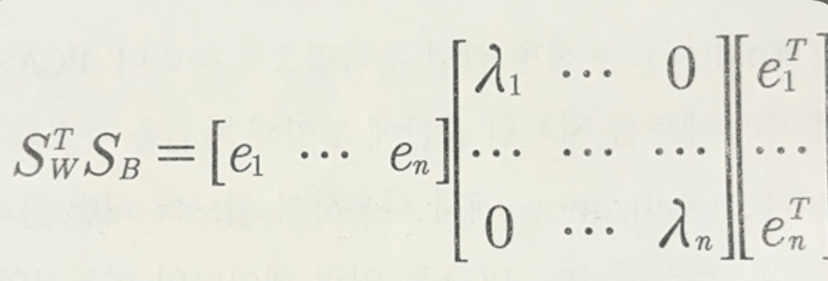
3. 고유값이 가장 큰 순으로 K개(LDA 변환 차수만큼) 추출

4. 고유값이 가장 큰 순으로 추출된 고유벡터를 이용해 새롭게 입력 데이터 변환

 

2. NMF(Non-Negative Matrix Factorization)

NMF

; Truncated SVD와 같이 낮은 랭크를 통한 행렬 근사(Low-Rank Approximation) 방식의 변형.

원본 행렬 내의 모든 원소 값이 모두 양수라는게 보장되면, 다음과 같이 간단하게 두 개의 기반 양수 행렬로 분해될 수 있는 기법 지칭

4 X 6 원본행렬은 4 X 2 행렬과 2 X 6 행렬로 근사해 분해가능

행렬 분해 → SVD과 같은 행렬 분해 기법 통칭.

⇒ 행렬 분해 하게 되면 일반적으로 길고 가는 행렬 W(원본 행렬의 행크기와 같고 열 크기보다 작은행렬)와 작고 넓은 행렬 H(원본 행렬의 행 크기보다 작고 열 크기와 같은 행렬)로 분해 됨.

분해된 행렬은 잠재 요소를 특성으로 가지게 됨,

분해 행렬 W는 원본 행에 대해 이 잠재 요소의 값이 얼마나 되는지에 대응,

분해 행렬 H는 이 잠재 요소가 원본 열(원본 속성)로 어떻게 구성됐는지를 나타내는 행렬.

 

ex. 사용자의 상품(영화 등) 평가 데이터 셋인 사용자-평가 순위 데이터 세트를 행렬 분해 기법을 통해 분해하면서 사용자가 평가하지 않은 상품에 대한 잠재적 요소를 추출해 이를 통해 평가 순위를 예측하고, 높은 순위로 예측된 상품을 추천해주는 방식. (잠재요소기반 추천방식)

 

*차원축소는 단순피처개수 줄이는 개념보다 데이터를 잘 설명할 수 있는 잠재적 요소 추출에 큰 의미가 있음.

→ 많은 차원 가지는 이미지나 텍스트에서 활발히 사용.

SVD(직사각행렬도 가능), NMF → 매우 많은 피처 데이터 가진 고차원 행렬을 두 개의 저차원 행렬로 분리하며 원본 행렬의 잠재된 요소 추출하기 땜에 토픽 모델링이나 추천시스템에서 사용됨.