GMM(Gaussian Mixture Model, MOG(Mixture of Gaussian Clustering)
k-means clustering : 거리 기반, discrete label
Gaussian Mixture : 확률 기반, probabilistic→responsibility (어떤 sample이 어떤 cluster에 얼마나 속하는지가 확률 값으로 나옴)
← 두 모델의 공통점은 iterative method라는 것.




- responsibility ← probability로 나타낸 cluster label, n번째 sample Xn이 k번째 cluster에 속할 확률
ex) 원래 k-means 에서는
R = [ 1 0 0 0
0 1 0 0
..] 였지만,
여기선,
r = [ 0.9 0.1 0 0
0.05 0.8 0.1 0.05
….]




-> 이게 GMM의 EM(Expectation and Maximization) 방식

원래 vector ver.일 때 sigma, covariance 이렇게 구했었으니까. 여기에 responsibility만 곱해주는 것.
정리)
GMM 군집화는 군집화를 적용하고자 하는 데이터가 여러 개의 가우시안 분포를 가진 데이터 집합들이 섞여서 생성된 것이라는 가정하에 군집화를 수행하는 방식.
여기서 가우시안 분포는, 정규 분포로도 알려진, 좌우 대칭형의 종 형태를 가진 통계학에서 가장 잘 알려진 연속 확률 함수임.
GMM은 데이터를 여러 개의 가우시안 분포가 섞인 것으로 간주함.
→ 즉, 전체 데이터 세트는 서로 다른 정규 분포 형태를 가진 여러 가지 확률 분포 곡선으로 구성될 수 있으며, 서로 다른 정규 분포에 기반해 군집화를 수행하는하는 것이 GMM 군집화 방식임.
**ex)
1000개의 데이터 세트가 있다면 이를 구성하는 여러 개의 정규 분포 곡선을 추출하고, 개별 데이터가 이 중 어떤 정규 분포에 속하는지 결정하는 방식임.

이 과정을 모수 추정이라 하는데, 모수 추정은 2가지를 추정함
- 개별 정규 분포의 평균과 분산 (M이랑 sigma(covariance))
- 각 데이터가 어떤 정규 분포에 해당되는지의 확률 (responsibility)
- GMM을 이용한 붓꽃 데이터 세트 군집화
GaussianMixture 객체의 가장 중요한 초기화 파라미터는 n_components(GMM모델의 총 개수)임. ← K-평균의 n_clusters와 같이 군집의 개수를 정하는 역할
from sklearn.mixture import GaussianMixture
gmm = GaussianMixture(n_components=3, random_state=0).fit(iris.data)
gmm_cluster_labels = gmm.predict(iris.data)
# 클러스터링 결과를 irisDF 의 'gmm_cluster' 컬럼명으로 저장
irisDF['gmm_cluster'] = gmm_cluster_labels
irisDF['target'] = iris.target
# target 값에 따라서 gmm_cluster 값이 어떻게 매핑되었는지 확인.
iris_result = irisDF.groupby(['target'])['gmm_cluster'].value_counts()
print(iris_result)
- GMM과 K-평균의 비교
K-평균은 평균 거리 중심으로 중심을 이동하면서 군집화를 수행하는 방식이므로 개별 군집 내의 데이터가 원형으로 흩어져 있는 경우에 매우 효과적으로 군집화 수행가능 → 원형 범위에서 군집화 수행
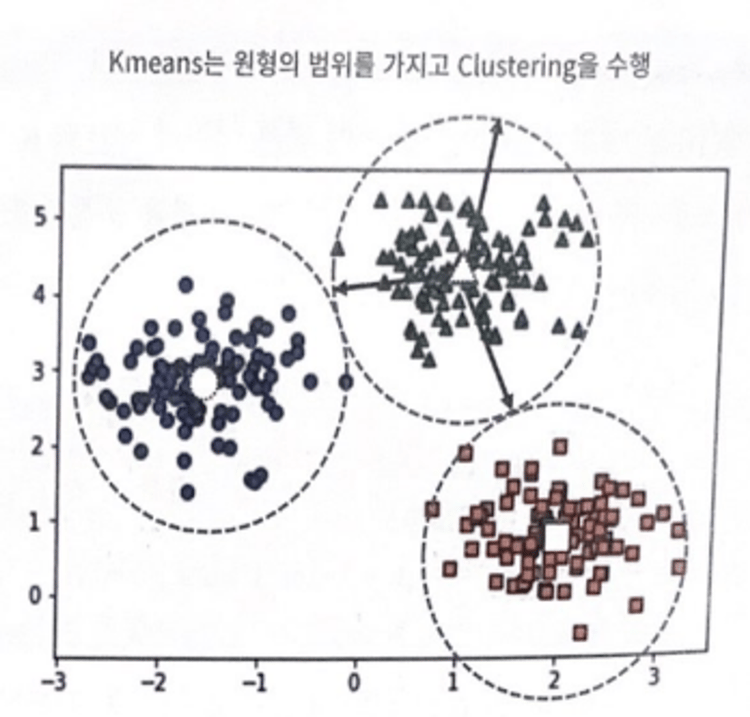
데이터가 길쭉한 타원형으로 늘어선 경우에 군집화를 잘 수행하지 못함
↔ GMM의 경우는 KMeans보다 유연하게 다양한 데이터 세트에 잘 적용될 수 있다는 장점이 있지만, 수행 시간이 오래걸림.
'Machine Learning > 군집화' 카테고리의 다른 글
| [파이썬 머신러닝 가이드] 군집화 - DBSCAN, 군집화 실습(고객 세그먼테이션) (2) | 2023.12.26 |
|---|---|
| [파이썬 머신러닝 가이드] 군집화 - 평균 이동 (2) | 2023.12.26 |
| [파이썬 머신러닝 가이드] 군집화 - 군집 평가 (Clustering Evaluation) (0) | 2023.12.25 |
| [파이썬 머신러닝 가이드] 군집화 - K Means 알고리즘 (1) | 2023.12.25 |

