전 게시물인 '[시계열 분석] 정상성' 에서도 알 수 있듯이, 시계열 데이터는 추세-주기, 계절성, 잔차의 합 혹은 곱으로 볼 수 있음.
[시계열 분석] 정상성
시계열 데이터 분석의 기본 전제가 되는 중요한 특성인 정상성에 대해 알아보자. 정상성 - 시간의 흐름에 관계없이 데이터의 평균 및 분산이 일정함을 의미하며, 이런 특성은 시계열 분석의 기
y8jinn.tistory.com
추세와 계절성이 명확히 드러나는 경우 -> 추세와 계절성, 잔차로의 분해만으로도 예측할 수 있으나,
명확한 추세와 계절성을 가지지 않는 주식이나 금값, 유가 등은 어떻게 예측할까?
=> 시계열 모델
ARIMA (AutoRegressive Integreted Moving Average) 모델
ARIMA 모델은 AR, MA, I 가 합쳐진 모델이다.
- 자기 회귀 모델 (AR) - 이전 관측 값이 이후 관측 값에 영향을 준다!

yt: t시점에서의 관측값 (시계열 데이터에서 현재 시점을 의미)
yt-1 : t-1 시점에서의 관측값
c : 상수항
φ : 자기 회귀 모델 계수 (과거가 현재에 미치는 영향을 나타내는 모수)
εt: 에러항(오차항), 백색 잡음
φ1yt-1 + ... + φpyt-p까지 값은 과거가 현재에 미치는 영향을 나타내는 모수 φ 에 시계열 데이터의 과거 시점을 곱한 것.
- 현재의 데이터를 과거의 데이터의 선형 결합으로 설명함.
- t시점의 데이터(yt)를 모델링할 때 y의 lag된 변수들(자신의 과거데이터)를 X 삼아서 회귀 모델을 만드는 것.
- 오늘의 값은 어제의 값 자체에 영향을 받음.
- 계수가 양수일 때는, 어제의 값이 큰 값이면 오늘의 값도 큰 값을 가지며,
음수일 때는, 어제의 값이 큰 값이면 오늘의 값은 작은 값이 됨.
- 자기 회귀 모델은 AR(p)로 표현하며, 여기서 차수 p는 p개의 과거 값들을 이용해 예측한다는 뜻.
- 이동 평균 모델 (MA)

yt : t시점에서의 관측값 (시계열 데이터에서 현재 시점을 의미)
c : 상수항
θ : 이동 평균 모델 계수
εt : t시점에서의 에러항(오차항), 백색 잡음
εt-1 : t-1 시점에서의 에러항(오차항), 백색 잡음
θ1εt-1 + ... + θqεt-q 까지의 값은 매개변수 θ 에 과거 시점의 오차를 곱한 것
- 트렌드(평균 혹은 시계열 그래프에서 y 값)가 변화하는 상황에 적합한 회귀 모델
- 현재의 데이터를 과거릐 데이터의 오차 항의 선형 결합으로 설명함.
- t 시점의 데이터 (yt)를 t 시점의 에러와 과거의 에러들로 표현함.
- 오늘의 값은 어제의 값의 오차항에 영향을 받음.
- 계수가 양수일 때는, 어제의 값이 상승하는 추세이면 오늘의 값도 상승하는 추세이며,
음수일 때는, 어제의 값이 상승하는 추세이면 오늘의 값은 하강함.
- 이동 평균 모델은 MA(q)로 표현하며, 여기서 차수 q는 q개 전 값부터 오차 값을 이용하겠다는 뜻.
- 차분(I)
AR과 MA 모델은 정상 시계열을 전제로 한 모델인데, 차분은 정상 시계열이 아닌 데이터를 정상화 시키는 방법 중 하나임.
- 1차 차분
1차 차분은 단순히 현재 시간과 그 전 시간의 차이, 즉 속도를 말함.
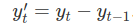
추세가 있어 증가 혹은 감소가 있는 시계열을 정상성을 갖지 않지만, 그 증가 속도, 감소 속도가 일정하다면 1차 차분을 통해 정상화 시킬 수 있음.
- 2차 차분

2차 차분은 속도와 속도의 차이이므로 가속도라고 생각해도 좋음.
결론적으로,
| AR (Auto-regressive) / AR(p) | AR(p) 모델은 p개의 과거 값들을 이용해 예측함 |
| MA (Mooving Average) / MA(q) | MA(q) 모델은 q개의 과거 오차 값들을 이용해 예측함 |
| ARMA (p,q) | ARMA(p,q) 모델은 p개의 과거 값과 q개의 과거 오차 값들을 이용해 예측함 |
| ARIMA (p,d,q) | 데이터를 d회 차분하고, p개의 과거 값과 q개의 오차 값을 이용하여 예측 그 후, 다시 비차분화 (차분화 값을 다시 원래의 값으로 변화)하여 예측값 생성 |
ARIMA 모델에서 변수 p,d,q의 의미
p : p개 전 값부터 과거 값 이용 (p개의 과거 값들 이용하여 예측)
d : d만큼 차분함
q : q개 전 값부터 오차 값 이용
- p, d, q 차수의 결정
1) 차분 차수 d : 시계열 plot을 보고(ADF 검정을 통해 p-value값 확인하거나) 정상성 여부 확인하고, 차분을 진행하고, 차분 후의 plot을 보고 여부를 확인
2) p,q의 경우는 보통 ACF(Autocorrelation function)와, PACF(Partial Autocorrelation function)을 보고 결정함.
| AR(p) 모델 적합 | MA(q) 모델 적합 | ARMA(p,q) 모델 적합 | |
| ACF 그래프 | 점점 작아진다 | 첫 값으로부터 q개 뒤에 끊긴다 | 점점 작아진다 |
| PACF 그래프 | 첫 값으로부터 p개 뒤에 끊긴다 | 점점 작아진다 | 점점 작아진다 |
from scalecast.Forecaster import Forecaster
import matplotlib.pyplot as plt
import pandas_datareader as pdr
f = Forecaster(y, x) #x는 date(시계열 값)
f.plot() #데이터 어떻게 생겼는지
f.plot_acf() #ACF 플롯
f.plot_pacf() #PACF 플롯
plt.show()
ex) ACF, PACF 플롯을 그렸을 때,
위 그림처럼
ACF 그래프가 점점 작아지고, PACF 그래프는 첫 값으로부터 1개 뒤 이후부터 파란상자 안에 값이 들어가며 그래프가 끊긴다면
-> AR(1) 모델을 활용하는 것이 가장 정확도가 높을 것.
Q. 최적의 (p,d,q) 값을 찾기 위해서는?
가능한 모든 (p,d,q) 값을 돌려보고 가장 높은 정확도를 주는 쌍을 고르기.
for 문을 통해 p,d,q가 각각 0부터 4까지의 값일 때 AIC 가 어느정도 되는지 보고 가장 낮은 값을 가진 p,d,q 쌍을 고르면 된다.
import itertools
p=d=q=range(0,5)
pdq = list(itertools.product(p,d,q))
for param in pdq:
try:
model_arima = ARIMA(data, order = param)
model_arima_fit = model_arima.fit()
print(param, model_arima_fit.aic)
except:
continue
- ARIMA 모델 설계
from statsmodel.tsa.arima.model.import ARIMA
p = 2 #AR의 차수
d = 0 #차분 차수
q = 1 #MA의 차수
model = ARIMA(data[coloumn], order = (p,d,q))
fitted_model = model.fit()
forecast = model_fit.forecast(steps=10) #미래 10일을 예측
original_scale_forecast = np.exp(forecast) #전처리 과정에서 시계열 데이터가 비정상성 가지고 있을 때(or 변동이 큰 데이터의 스케일을 줄여주어 모델 학습 안정화 시키기 위해), 데이터를 안정적인 형태로 변환하기 위해 로그 변환 했다면 원래대로 되돌려주기'Deep Learning & AI > Time-Series' 카테고리의 다른 글
| [Paper Review] Time Series Forecasting (TSF) Using Various Deep Learning Models (2) (0) | 2024.05.13 |
|---|---|
| [Paper Review] Time Series Forecasting (TSF) Using Various Deep Learning Models (1) (0) | 2024.04.01 |
| [시계열 분석] 정상성 (0) | 2024.02.19 |
| 순서가 있는 데이터를 위한 딥러닝 기본 - RNN BPTT (1) | 2024.02.12 |
| 순서가 있는 데이터를 위한 딥러닝 기본 - RNN 핵심 이해 (1) | 2024.02.11 |

