목차
논문의 목적
- time series 데이터에 대해 RNN, LSTM, GRU, Transformer 4개의 모델들을 학습 및 평가하여 비교한다.
- 각 모델들의 강점과 약점을 평가한다.
- w, k의 영향력을 정확도 측면에서 이해해본다.
Ⅰ. Introduction
Time Series Forecasting (TSF)는 과거의 observations로부터 미래 시점의 예측 변수 분포를 예측하는 문제이다.
- traditional models
- linear : ARMA (stationary일 경우), ARIMA (non-stationary일 경우 차분을 해서 데이터가 정상성을 가질 수 있게)
- non-linear : ARCH, GARCH
💡 Stationarity(정상성)이란?
- 어떠한 시점에서도(시간의 흐름에 관계 없이) 데이터의 평균 및 분산이 일정함을 의미하며, 이런 특성은 시계열 분석의 기본 전제가 됨
- 누적이나 추세가 있는 값이 아니라, 확률변수 간의 확률 분포가 시간에 상관없이 일정한 성질을 띠고 있는 것이며, 시계열의 특징이 관측된 시간과 무관하다는 것
- machine learning models
- SVM
- deep learning models
- ANN
- RNN
- LSTM
- GRU
- Transformer
- 전통 통계 모델의 문제점
- 가장 최근의 데이터로부터 고정된 요인들만으로 회귀 예측하는 것
- 반복적(iterative)이며, 종종 프로세스가 어떻게 시작되는지 씨드(seed)에 매우 민감함
- 시계열 분석의 전제가 되는 정상성은 엄격한 조건이며, 드리프트(drift), 계절성(seasonality), 자기상관성(autocorrelation), 이분산성(heteroskedasticity) 등의 문제를 해결하는 것만으로는 변동성이 있는 시계열의 정상성을 이루기 어려움
-> 논문에서는 이러한 문제점들을 지적하며 그래서 머신러닝 모델이 필요하다고 말하고 있음
-> 머신러닝 모델에서는 SVM 모델을 언급하며 SVM과 ANN이 전통 통계모델보다 성능이 좋았으며, RNN, LSTM, GRU, 그리고 attention 기반 모델인 트랜스포머까지 해당 task에 아주 잘 맞아 좋은 성능을 내었다고 말하며 이러한 딥러닝 모델들을 중심으로 시계열 데이터 분석을 진행할 것이라 언급함
하지만 문제는,,
** 얼만큼의 과거 data(w)를 input 할지? **
** 얼만큼의 데이터(k)를 forecasting 할지? **
- Dataset
- UCI website의 “Beijing Air Quality Dataset”
- 2010년부터 2014년까지 5년 동안 시간 별로(hourly) 측정된 다변량 시계열 데이터
Ⅱ. Methodology
ŷ𝒕+𝒌 = 𝑓𝑘(𝑥𝑡−𝑤, … , 𝑥𝑡−1, 𝑦𝑡−𝑤, … , 𝑦𝑡−1)
- ŷ𝒕+𝒌: t+k 시간의 타겟 예측 변수 ( k:타겟 변수가 예측할 미래 시간의 길이)
- 𝑥𝑡−𝑤, … , 𝑥𝑡−1 : t-w 부터 t-1 시간에 이르기까지의 input vector
- 𝑦𝑡−𝑤, … , 𝑦𝑡−1 ∶t-w 부터 t-1 시간에 이르기까지의 타겟 예측 변수
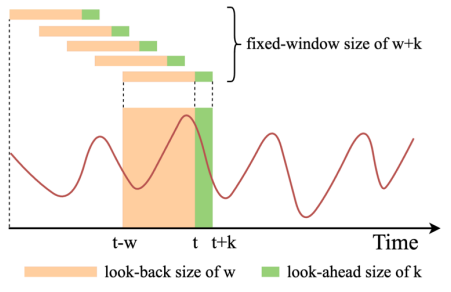
- time-series에서 input 데이터의 크기를 정하기 위해서는 look-back window 사이즈 w를 정할 수 있음 (얼만큼의 과거 데이터 가져올건지)
- output 데이터의 크기를 정하기 위해서는 k를 정할 수 있음 (input data로부터 얼만큼의 미래를 예측할지)
- 데이터는 min-max scaling으로 표준화 한 뒤, w만큼의 데이터가 input되어 k 시점만큼 예측하도록 전처리 됨
=> 각 모델마다 w와 예측할 k 크기의 관계를 조사함
Ⅲ. Deep Learning Frameworks
RNN (Recurent Neural Networks)
- RNN 계열의 알고리즘의 특징
- 계속해서 과거 정보들을 update하여 옮겨주는 컨베이어 벨트 역할을 하는 cell state라는 main stream을 모두 가지고 있음
- 이전 시점들의 데이터를 계속해서 update 해 나가면서 현재 시점의 데이터와 고려하여 예측하고, main stream을 업데이트 해 나가는 방식
- 과거의 정보들과 현재 데이터를 고려한 cell state는 다음 시점의 데이터를 예측하기 위해 입력으로 다시 들어가고, 다시 update되는 recurrent method 알고리즘
=> 이전 정보들이 순환, 반복하여 입력되어 이전 시점의 정보를 다 가지고 현 시점의 y를 예측하는 모델



- t = 시점
- 𝑺𝒕 = 과거 시점들로부터 계속해서 받아오는 값들을 고려하여 생성되는 벡터 (컨베이어 벨트 역할을 하는 mainstream)
=> RNN은 이전 시점의 데이터 S𝑡−1 를 hidden state로 받아 현재 입력 𝑥𝑡 와 결합시키고(식을 보면 둘이 summation 되어 있음), 가중치 𝑊𝑥𝑠 와 파라미터로 𝑺𝒕 생성함, 그리고 마지막엔 생성한 St에 한 번 더 layer를 통과시켜 비선형성이 가해진 뒤 sigmoid 함수를 통해 yt를 예측함
but, 사용되는 활성화 함수가 tanh과 sigmoid이기 때문에 기울기 소실 문제가 너무 빨리 와서 장기 과거 시점에 대한 모델 파라미터 업데이트가 안됨 (모델 학습이 안됨)
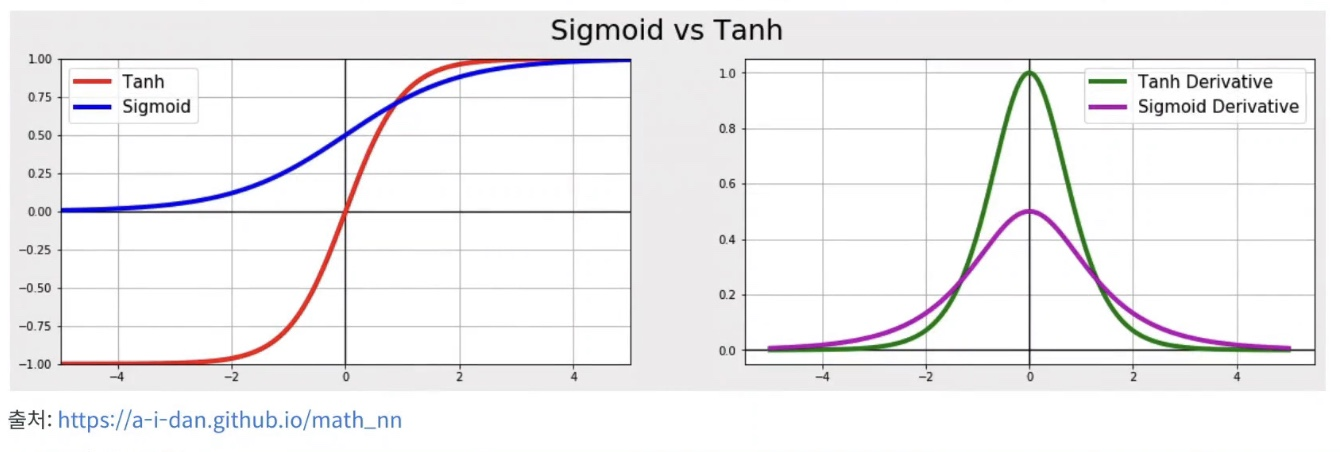
tanh 함수는 그림에서도 볼 수 있듯이 -1에서 1 사이의 값을 가지고, 미분하면 0과 1 사이의 값을 가지기 때문에 chain rule을 통해 계속해서 곱해지는 과정에서 계속 값이 작아짐, sigmoid 함수도 마찬가지!
-> 파라미터를 구해나가는 과정에서 기울기 소실 문제가 너무 빨리 오는 것
LSTM (Long Short-term Model)
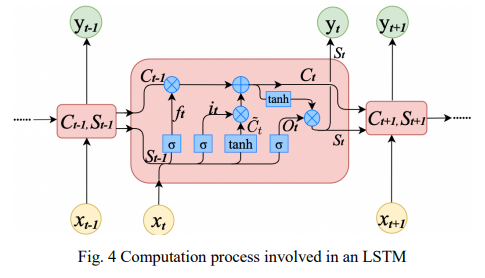
보통 2개의 stream을 Ct와 ht로 표현하는데 여기서는 ht 대신 St로 표현함
- 𝑪𝒕 = 과거 시점들로부터 계속해서 받아오는 값들을 정리하여 (정보를 선택적으로 활용) 인코딩한 벡터들에 집중
- 𝑺𝒕 = 현 시점의 인풋 데이터와 함께 과거 시점의 데이터를 어떻게 가용하여 y를 예측할지 더욱 고민하는 stream
=> 𝑪𝒕 가 이전 시점들의 정보들을 정리해오면, 𝑺𝒕 는 지금 받아온 현 시점의 정보 Xt를 어떻게 𝑪𝒕 에 적용할지 고민하고 예측까지 하는 것
- gate = 얼마나 정보를 활용하고 어떻게 정보를 활용할지 표현하는 layer

1) 𝒇𝒕 는 forget gate(불필요한 과거 정보를 잊기 위한 gate)로 이전 시점인 𝑺𝒕−𝟏과 𝑥𝑡 를 concat한 뒤, sigmoid layer에 넣음 (현 시점의 입력 데이터를 고려하여 지금까지 만들어온 𝑪𝒕−𝟏 데이터를 얼마나 기억할지 정하기 위해 0~1사이의 값으로 만든 뒤 (sigmoid로) 𝑪𝒕 에 곱해짐, 0에 가까울수록 정보를 많이 줄이는 것, 과거 cell state에서 사용하지 않을 데이터에 대한 가중치를 둠)
2), 3) 𝒊𝒕 는 input gate로 다음 𝑪෪𝒕 (임시 cell state)에 곱해지기 때문에 현 시점의 𝑥𝑡 데이터를 얼마나 기억할지 정하는 역할을 함 (따라서 이 layer도 0~1사이의 값으로 강제하기 위해 sigmoid 함수 적용, cell state에서 사용할 데이터를 저장하기 위한 가중치)
𝑪෪𝒕 는 t𝑎𝑛ℎ 함수 거쳐서 -1 ~ 1로 강제되어 4)에서 𝒊𝒕 에서 나온 벡터와 곱해짐. (0~1사이로 강제된 값은 그 벡터의 영향력을 의미한다면, -1 ~ 1로 강제된 값은 그 벡터의 방향성을 의미하고 두 벡터가 multiplication 됨, 종합적으로 음수쪽으로 영향력이 강한 벡터일수록 -1의 값을 갖고, 양수쪽으로 영향력이 강한 벡터일수록 1의 값을 갖게 되는 식으로 인코딩 됨)
4) 𝑪𝒕 는 이 때까지 입력한 시퀀스 데이터를 전부 고려하여 벡터를 만들어가는 𝒔𝒕𝒓𝒆𝒂𝒎
(각 원소들은 현재 들어온 𝑥𝑡 값을 고려하여 임팩트가 강한 값들 위주로 기억하고 있음)
5), 6) 𝑶𝒕 는 output gate로 최종 y를 예측하는 게이트임. main stream의 𝑪𝒕 를 현재 입력값인 𝑥𝑡 와 다시 한 번 인코딩하여 𝒚𝒕 를 예측하기 직전까지 감. (이 때, 두 벡터를 인코딩할 때 𝑥𝑡 는 forget gate처럼 그 영향력을 고려하기 위해 sigmoid layer를 거친 값이고, 𝑪𝒕 는 음, 양의 영향력을 고려하기 위해 tanh 활성화 함수를 거친 값임, 𝑶𝒕는 hidden state에 cell state를 얼마나 반영할 것인지에 대한 가중치를 둠 )
7) 𝒚𝒕 를 예측g하기 위한 output gate의 마지막 layer로 5)에서 만든 벡터를 최종적으로 비선형성을 한 번 더 가해주기 위해 sigmoid를 활성화 함수로 하는 최종 layer를 통해 𝒚𝒕 예측함
=> 이처럼 lstm은 학습해야 할 파라미터와 과정이 복잡하기 때문에 기울기 소실 문제를 해결할 수 있음.
과거 시점의 정보들을 여러가지 gate를 통해 비선형성도 높이고, 더욱 효율적으로 활용하기 때문에 RNN에 비해 더욱 긴 시점의 정보들을 좀 더 미세하게 컨트롤하는 것.
GRU (Gated Recurrent Unit)
복잡한 LSTM 모델을 좀 더 단순화하여 파라미터 개수를 줄이는 모델임.
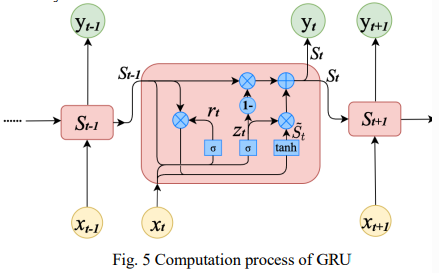
- forget gate, input gate를 update gate (𝒛𝒕)로 통합, output gate를 없애고 reset gate (𝒓𝒕) 정의
- cell state, hidden state를 hidden state(𝑺𝒕)로 통합

1) 𝒓𝒕 는 reset gate로 현재 입력 데이터인 Xt와 여태까지 정보를 잘 담아온 main stream St-1 벡터를 서로 sum하여 layer에 입력하여 sigmoid 함수를 거쳐 나옴. (0에서 1 사이의 스케일로 강제되기 때문에 데이터에 대해 얼마나 잊을지 확률화 하는 과정)
2), 3) update gate 또한 파라미터는 다르지만 비슷한 방식으로 계산되고 있음. 그리고 1번식에서 만든 reset gate를 가지고 임시 St를 계산해줌
4) 계산한 임시 St를 이용하여 main stream St를 계산하고 있음
💡 𝒛𝒕 가 현재 정보를 고려한 중요도이기 때문에, (1- 𝒛𝒕) 는 과거 정보의 중요도임
(1- 𝒛𝒕) 는 lstm의 forget gate의 역할을 하며 이제껏 정보를 정리해온 main stream 𝑺𝒕−𝟏벡터와 곱해지고, 𝒛𝒕 는 lstm의 input gate 역할을 하며 tanh 활성화 함수를 거쳐 -1 ~1 스케일로 강제된 ෪𝑺𝒕 벡터와 곱해짐 (LSTM의 forget gate와 input gate를 동시에 하는 느낌)
결론적으로,
RNN, LSTM, GRU 모두 현재를 예측할 때 과거정보를 이용하여 순서가 있는 데이터에 특화된 모델이지만, hidden state, 여기서는 St를 구하는 방식이 다르다는 차이가 있음.
RNN은 과거의 hidden vector들이 과거의 정보를 담고 있으니, 과거 hidden vector를 현재 hidden vector에 계속 결합해서 사용하는 것이고, St를 현재 정보와 과거 hidden state의 결합으로 구함.
LSTM은 gate를 이용해서 과거의 정보를 얼만큼 이용할 것인지, 어떤게 중요하고 아닌지를 weight로 조정하여 현재정보까지 고려하는 것.
GRU는 과거와 현재정보를 control하는 건 LSTM과 동일한데, hidden state를 구하는 복잡한 과정을 단순화 시켰다는 차이점이 있음.
Transformer
: 앞선 모델들과 다르게 RNN을 사용하지 않고, Encoder-Decoder를 따르면서도 attention만으로 구현된 모델

1) Positional Embedding
encoder에 있는 부분
Transformer 모델은 RNN과 다르게 데이터를 한 번에 읽을 수 있도록 구현한 모델임
-> 모델에게 데이터, 벡터의 위치 정보를 알려줄 필요가 있기 때문에 positional embedding을 사용해서 각각의 위치정보를 입력해주게 됨.
2) Multi-head Self-Attention in Encoder

Transformer 모델의 핵심 내용을 담고 있는 부분으로, 그림을 보면 animal과 it이 진한색의 색으로 연결되어 있음.
self-attention의 역할은 전체 입력 데이터에서 벡터끼리의 유사도를 이용하여 가장 연관성이 높은 벡터를 찾아내는 것.
3) Masked Multi-head Self-Attention in Decoder
Masked Multi-head Attention은 decoder에만 존재하는 모듈로 RNN의 연산 룰을 지니고 있음
Encoder에 있는 Multi-head Attention의 경우, self attention 연산 시에 모든 벡터들과의 연관성에 대해 연산을 진행하므로 Bi-directional(양방향성)임
하지만, Decoder의 경우는 정답을 도출하는 부분으로써 RNN과 동일하게 순차적으로 데이터를 읽어올 수 있으며 앞의 생성되는 벡터는 뒤의 벡터를 볼 수 없도록 구현하며, Uni-directional(단방향성)을 가짐
=> 따라서 앞에 등장하는 벡터가 뒤에 벡터를 보지 못하게 masking 이라는 작업을 진행하게 되는 것
4) Multi-head Self-Attention in Decoder
multi-head attention이라는건 Encoder 에도 존재했는데, 이 둘은 연산적인 부분에서 차이점은 없고, 유일한 차이점은 입력 데이터임.
Decoder에 있는 multi-head attention은 인코더에서와 다르게 인코더로부터 얻은 값도 존재하고, 디코더로부터 얻은 값도 존재함.
-> 해당 연산을 통하여 인코더에서 얻은 정보를 디코더로 넘겨주는 역할을 진행
5) FeedForward Network
2층으로 된 linear projection layer이며, 단순 MLP 연산과 동일
여기까지가 논문 소개 및 사용할 딥러닝 모델 프레임워크를 소개하는 내용이었고,
이어서 다음 포스팅에 이러한 딥러닝 모델을 기반으로 시계열 데이터에 접목시켜 모델의 성능과, w,k의 영향력을 비교해 보겠다.
'Deep Learning & AI > Time-Series' 카테고리의 다른 글
| [Paper Review] Time Series Forecasting (TSF) Using Various Deep Learning Models (2) (0) | 2024.05.13 |
|---|---|
| [시계열 분석] ARIMA(AutoRegressive Integreted Moving Average) - 자기 회귀 누적 이동 평균 모델 (0) | 2024.02.26 |
| [시계열 분석] 정상성 (0) | 2024.02.19 |
| 순서가 있는 데이터를 위한 딥러닝 기본 - RNN BPTT (1) | 2024.02.12 |
| 순서가 있는 데이터를 위한 딥러닝 기본 - RNN 핵심 이해 (1) | 2024.02.11 |

